Part 5: Which point did I just click? implementing range queries on 2D space
A fundamendal scenario in GUI design applications is the user manipulating objects with their mouse. The application must be able to tell which object is underneath the cursor to enable manipulation or simply highlighting the object when the user hovers over it. For a small amount of objects a linear search will do fine. In gerb’s case we want to interact with the control points and handles of the splines of a glyph. I suspect that even for a complex glyph with lots of curves, a linear search might not be that bad; but since we will be performing such queries multiple times a second when the user is moving their mouse, it’s a good idea to start with a basic performant approach for this problem.
Problem statement
Given a (possibly dynamic) list of points on a 2 dimensional coordinate system and some kind of identifier for each point, we want to be able to query the points within a given 2D range (a rectangle) in the grid.
The k-d tree data structure
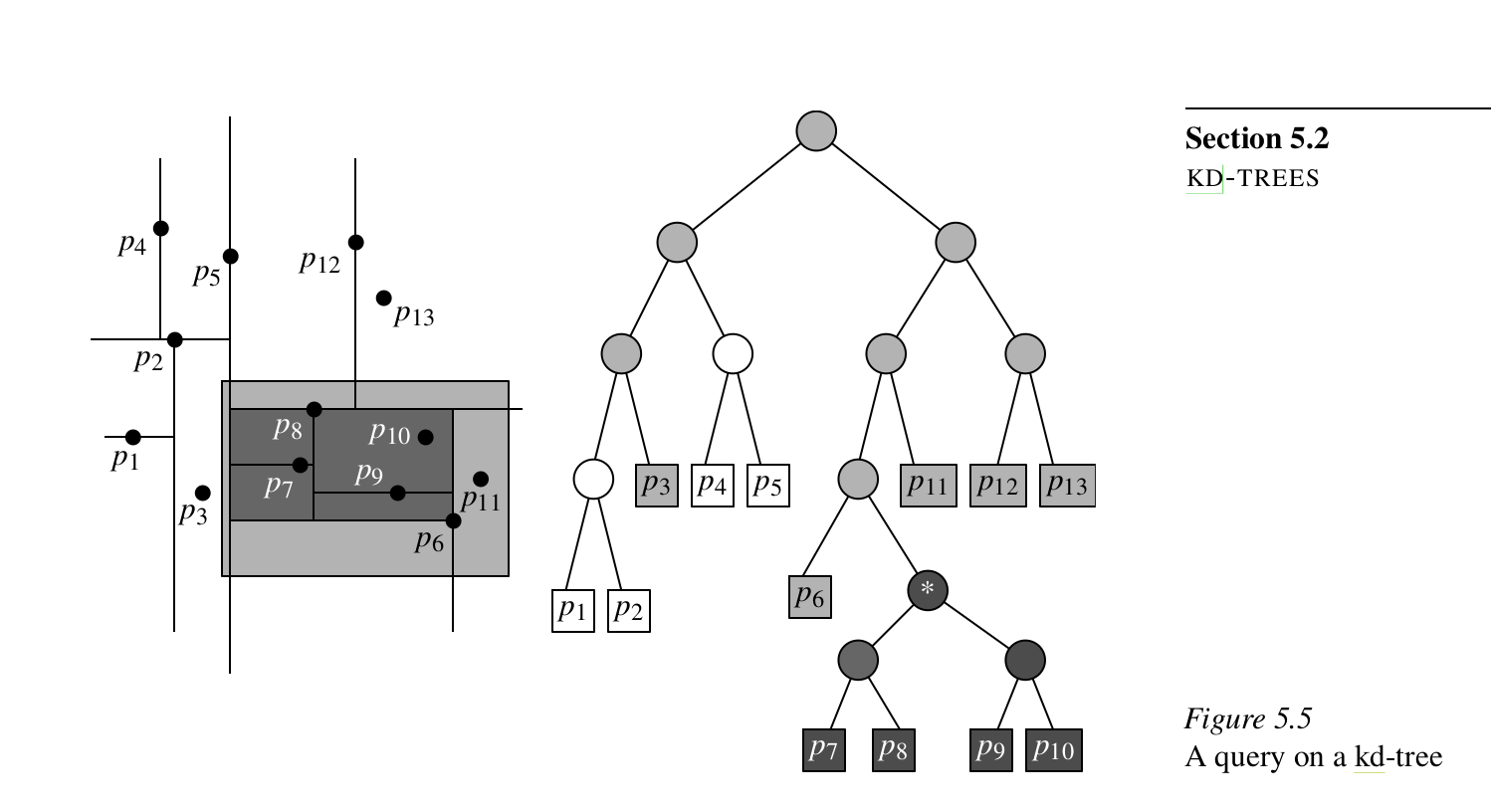
The k-d tree is a tree graph where each node represents a 2D subrectangle of the total area defined by the given points and each level of the tree (The level of a node is the number of edges along the unique path between it and the root node) when summed up contains the entire area. Each node distributes its subrectangle into its children based on some rule and therefore at each level the area gets broken into smaller and smaller rectangles, until only leaf nodes that contain a point or a group of points are left. The rule could for example be splitting the rectangle in half, in which case we would have a binary partition tree.
In this implementation, a node N is assigned to split its points into two groups by checking the x or y coordinate if its level is an even or odd number and compare it to the median x or y coordinate of the group.
Source code
References:
- Computational Geometry: Algorithms and Applications